Set

A set is a collection of objects. Each such objects are known as set elements.

E.g.: A set of vowels represented as:

$$A=\{a,e,i,o,u\}$$

E.g.: A set of positive integers represented as:

$$A=\{0,1,2,3,...\}$$

Set Notation

There are two kinds of set notations:

1. Tabular method
2. Set builder method

Tabular method

When the set is written with the actual data of elements, the form is said to be tabular.

E.g.: A set of positive integers:

$$A=\{0,1,2,3,...\}$$

Set builder method

When the set is written in a generalized way, which denotes all available set elements within it, the form is said to be set builder.

E.g.: A set of positive integers:

$$A=\{x|x\geq0,x\in{Z}\}=\{x|x\in{Z^+}\}$$

E.g. A set of numbers divisible by 5:

$$A=\{x|x\textnormal{ MOD }5=0,x\in{Z^+}\}$$

Example 1: Write a set of letters of the word $GOOGLE$ in both set builder and tabular form.

In tabular form:

$$A=\{G,O,L,E\}$$

In set builder form:

$$A=\{x|x\in{A}\}=\{x|x\in\{G,O,L,E\}\}$$

Example 2: Write the set $B=\{x|x\in{Z^+},z\leq9\}$ in tabular form.

In tabular form:

$$B=\{0,1,2,3...9\}$$

Subset

Let $A$ and $B$ be two sets. If every element of $A$ is also an element of $B$, then $A$ is a subset of $B$, and is written as $A\subseteq{B}$.

E.g.: Consider the following two sets $A$ and $B$:

$$A=\{2,3,4\}$$ $$B=\{1,2,3,4\}$$

Since, all elements of $A$ are in $B$, therefore $A\subseteq{B}$.

A set is also its own subset.

Power Set

Let $A$ be a set containing $n$ elements. The set of all subsets of $A$ is called the power set of $A$. It consists of $2^n$ elements. It power set of set $A$ is denoted as:

$$\mathcal{P}(A)$$

E.g.: Considering the set $A=\{a,b,c\}$, then its powerset will be:

$$\mathcal{P}(A)=\{\{a\},\{b\},\{c\},\{a,b\},\{b,c\},\{a,c\},\{a,b,c\},\{\phi\}\}$$

Null set $\phi$ is a subset of every set.

The following relations between numbers always hold true:

$$N\subseteq{Z}\subseteq{R}$$

where,

• $N$: natural numbers
• $Z$: integer numbers
• $R$: real numbers

Compliment of a Set

Let $A$ and $B$ be two sets. The set consisting of all elements of $B$, which are not in $A$, is called compliment of $B$, and is denoted as $B-A$.

Considering the following sets as an example:

$$B=\{5,9,8,12,15\}$$ $$A=\{9,8,11,15\}$$

Then, the compliment of $B$ would be:

$$B-A=\{5,12\}$$

Basic Operations on Sets

Following are the operations on sets:

1. Union
2. Intersection
3. Symmetric difference

Union

Let $A$ and $B$ be two sets. The set consists of all elements of $A$ or $B$ or both, is called the union of $A$ and $B$. It is written as $A\cup{B}$.

Figure 1: Venn diagram for $A\cup B$:

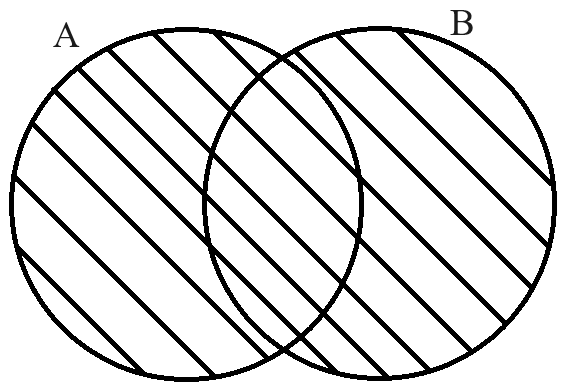
E.g.: Considering two sets: $B=\{5,9,8\}$ and, $A=\{1,5,9,3\}$. Their union would be:

$$A\cup{B}=\{1,3,5,8,9\}$$

Intersection

Let $A$ and $B$ be two sets. The set elements which are both in $A$ and $B$ defines the intersection of $A$ and $B$. It is written as $A\cup B$.

Figure 2: Venn diagram for $A\cap B$:

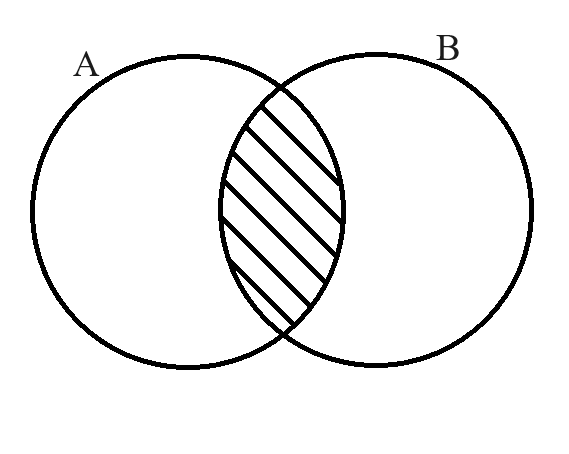
E.g.: Considering two sets:

$$A=\{1,5,9,3\}$$ $$B=\{5,9,8\}$$

Then, $A\cap B=\{5,9\}$

Symmetric difference

Symmetric difference between two sets $A$ and $B$ is defined by the set of all elements that belong to $A$ or $B$, but not to both. It is denoted by $A\bigoplus B$.

Figure 3: Venn diagram for $A\bigoplus B$:

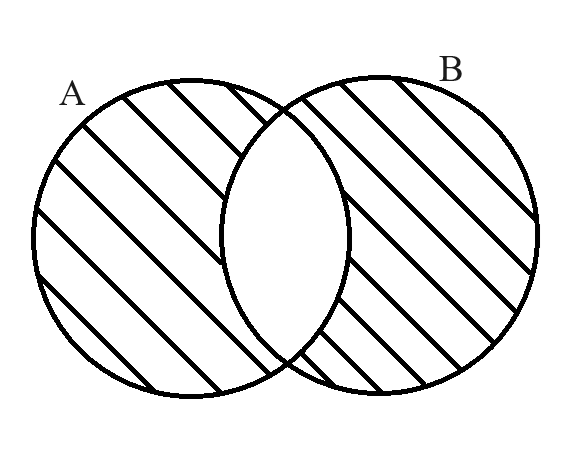
E.g.: Considering $A=\{1,5,9,3\}$ and, $B=\{5,9,8\}$. Then, $A\bigoplus B=\{1,3,8\}$

Example 3: If $A=\{1,2,3,4\}$, and $B=\{1,3,5,7,11\}$. Then prove that $A\bigoplus B=(A-B)\cup(B-A)$.

$$\textnormal{LHS}=A\bigoplus B=\{2,4,5,7,11\}$$ $$\textnormal{RHS}=(A-B)\cup(B-A)\\=\{2,4\}\cup\{5,7,11\}\\=\{2,4,5,7,11\}$$ $$\therefore A\bigoplus B=(A-B)\cup(B-A)$$

$\therefore \textnormal{LHS}=\textnormal{RHS}$, hence proved.

Principle of Inclusion and Exclusion

Let us suppose there are two sets $A$ and $B$, and they share elements between each other. If we want to find the total no. of elements in $A$ and $B$, without repeating any common element, then the principle of inclusion and exclusion states the following:

$$|A\cup B|=|A|+|B|-|A\cap B|$$

The number of elements of $A$ is added with all elements in $B$. The sum is then subtracted from the common elements in $A$ and $B$, which was added twice.

Principle of inclusion and exclusion of three variables

Let the three sets be $A$, $B$, and $C$.

Then,

$$|A\cup B\cup C|=|A\cup(B\cup C)|\\ =|A|+|B\cup C|-|A\cap(B\cup C)|\\$$

By distributive law, we know that $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$. Therefore,

$$=|A|+|B|+|C|-|B\cap C|-|(A\cap B)\cup(A\cap C)|\\ =|A|+|B|+|C|-|B\cap C|-\{|A\cap B|+|A\cap C|-|A\cap B\cap A\cap C|\}\\$$

Since, $A\cap A=A$, therefore:

$$=|A|+|B|+|C|-|B\cap C|-\{|A\cap B|+|A\cap C|-|A\cap B\cap C|\}\\ =|A|+|B|+|C|-|B\cap C|-|A\cap B|-|A\cap C|+|A\cap B\cap C|$$

Therefore,

$$(A\cup B\cup C)=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$$

Practice questions

1. Let $U=\{x|x\in Z^+,x\leq9\}$, $A=\{1,3,5,7\}$, $B=\{2,4,6\}$, and $C=\{1,2,3,4\}$. Find:
   • (a) $A\cap B$ and $A\cap C$
   • (b) $A\cup B$ and $B\cup C$
   • (c) $\bar{B}$ and $\bar{C}$
   • (d) $A\bigoplus B$ and $B\bigoplus C$
   • (e) $(A\cup C)-B$, $A\cup B$, $(B\bigoplus C)-A$
2. Using Venn diagram, show the following sets:
   • (a) $(A\cup B)\cap C$
   • (b) $A-(B-C)$
   • (c) $A\cap(B\bigoplus C)$
   • (d) $A-(B\cup C)$
   • (e) $\bar{A}\cap(C-B)$
   • (f) $\bar{A}\cap(B\cap C)$
3. Answer the following questions:
   • (a) If $A=\{6,2,3\}$, find $\mathcal{P}(A)$.
   • (b) What is $|A|$ and $|\mathcal{P}(A)|$?
4. Let $U=\{x|x\in Z^+,x\leq9\}$, $A=\{1,2,4,6,8\}$, $B=\{2,4,5\}$, $C=\{x|x\in Z^+,x^2\leq9\}$, and $D=\{7,8\}$. Compute the following:
   • (a) $A-B$
   • (b) $B-A$
   • (c) $\bar{C}$
   • (d) $B\bigoplus C$
   • (e) $C\bigoplus D$
   • (f) $\bar{A\cup B}$
   • (g) $A\cap(\bar{C}\cup D)$
5. In MIT, from a batch of 125 students, 100 students of Mathematics opt for one of the following languages: PASCAL, FORTRAN, and C++. 45 students opt for PASCAL, 25 students opt for FORTRAN, 10 students opt for C++, 5 students opt for both PASCAL and FORTRAN, 20 students opt for both FORTRAN and C++, 7 students opt for PASCAL and C++. Answer the following questions:
   • (a) How many students study all languages?
   • (b) How many students study only FORTRAN?
   • (c) How many students do not study any of the languages?