A function assigns exactly one element of a set to each element of the other set. Functions are the rules that assigns one input to one output. The function can be represented as $f:A\to B$. $A$ is called the domain, and $B$ is called the co-domain.

Figure 1: Relation map between domain $A$, and co-domain $B$:

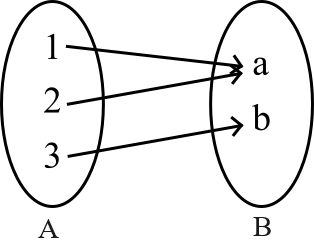
Range

The elements of the co-domain that are participating in the function is called range. For example, in the following figure:

Figure 2: Relation map between domain $A$, and co-domain $B$:

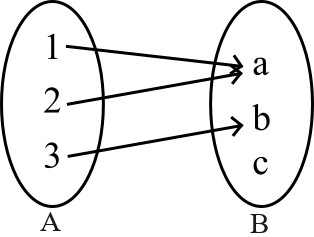
The range of the function are only those elements participating in the function. The range $R$ is:

$$R=\{a,b\}$$

It is important to note that, any range is a subset of the co-domain, i.e.,

$$R\subseteq B$$

where, $R$ is the range, and $B$ is the co-domain.

Example 1: State if the following are functions or not.

1. $f(x)={1\over x}$, where $x\in R$.

   This is not a function, as for $x=0$, the function $f(x)=f(0)$ is not defined.

2. $f(x)=\sqrt{x}$, where $x\in R$.

   This is not a function, as for any negative value of $x$, the function $f(x)$ is not defined.

3. $f(x)=\pm{\sqrt{x^2-1}}$, where $x\in R$.

   This is not a function, as there are two possible values for $f(x)$, A function should only have, or point to one value.

Example 2: Given two sets, $A=\{p,q,r,s\}A={p,q,r,s}A=\{p,q,r,s\}A={p,q,r,s}$, and $B=\{a,b,c\}B={a,b,c}B=\{a,b,c\}B={a,b,c}$. Draw the function diagram and determine whether, the relation is a function or not. If it is a function, determine the range, domain and co-domain, for the following:

(1) $\{(p,a),(q,a),(r,a),(s,a)\}$,

(2) $\{(p,a),(q,b),(p,b),(r,a),(s,b)\}$.

Solution

1. The relation map for the function is:

   

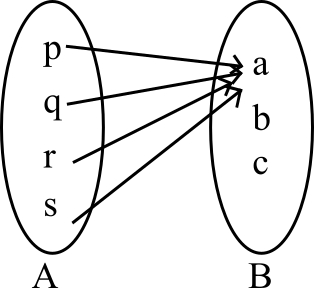
   It is a function.

   Range, $R=\{a\}$

   Domain, $D=\{p,q,r,s\}$

   Co-domain, $D'=\{a,b,c\}$

2. The relation map for the function is:

   

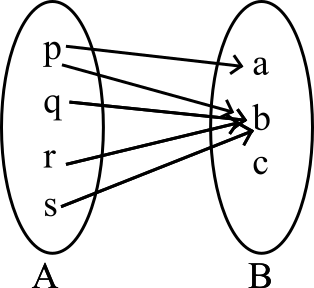
   It is not a function, since $p$ returns two different values.

Types of Functions

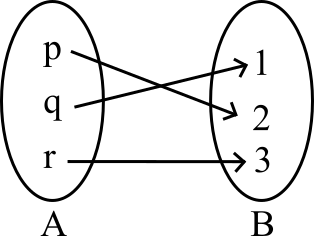
One to one function: Injective function

A function $f:A\to B$ is said to be one to one function if different elements of $A$ have different images in $B$.

Figure 3: Relation map between an one to one function of $A$ and $B$:

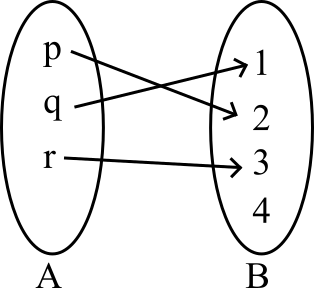
Onto function: Subjective function

A function $f:A\to B$ is said to be onto function if every element of $B$ is an image of some element of $A$, i.e., the range of $f$ is equal to its co-domain.

Figure 4: Relation map between an onto function of $A$ and $B$:

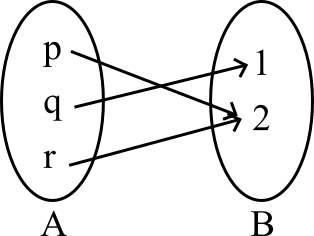
One to one correspondent function: Bijective function

A function $f:A\to B$ is called one to one correspondent function if the function is both one to one and onto function.

Figure 5: Relation map between an one to one correspondent function of $A$ and $B$:

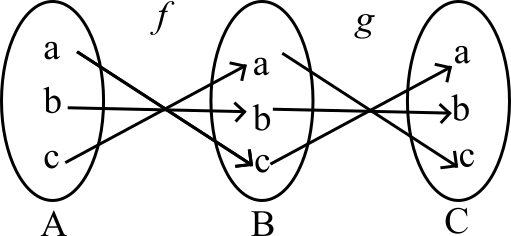
Composition of a Function

Let $f:A\to B$ and $g:B\to C$ be two function such that range of $f$ is a subset of domain of $g$, then a new function $gof: A\to C$, called the composition of $f$ and $g$ may be defined as:

$$gof(a)=g(f(a))\ \forall\ a\in A$$

Figure 6: Relation map for composition of a function between $A$, $B$, and $C$:

For $fog$:

• $f(g(a))=f(c)=a$

• $f(g(b))=f(b)=b$

• $f(g(c))=f(c)=c$

For $gof$:

• $g(f(a))=g(c)=a$

• $g(f(b))=g(b)=b$

• $g(f(c))=g(a)=c$

Example 3: Let $f:R\to R$ be a function defined by $f(x)=x^3$, and $g:R\to R$ be a function defined by $g(x)=x-1$. Compute $fog$ and $gof$ and find if they are equal or not.

Solution:

$$fog=f(g(x))=f(x-1)=(x-1)^3=x^3-3x^2+3x-1$$

and,

$$gof=g(f(x))=g(x^3)=x^3-1$$

It is found that:

$$fog\neq gof$$

Example 4: Let $f(x)=3x+1$, and $g(x)=x^2$. Find out $fog$, and $gof$.

Solution:

$$fog=f(g(x))=f(x^2)=3x^2+1$$

and,

$$gof=g(f(x))=g(3x+1)=(3x+1)^2=9x^2+6x+1$$

Example 5: Let $f(x)=3x^2$. Find $fof$.

Solution:

$$fof=f(f(x))=f(3x^2)=3(3x^2)^2=27x^4$$

Example 6: Let $f(x)=x$, $g(x)=2x$, and $h(x)=3x$. Find $fogoh$, when $x=-1$.

Solution:

$$fogoh=f(g(h(x)))=f(g(3x))=f(6x)=6x$$

When, $x=-1$

$$\therefore fogoh=6(-1)=-6$$