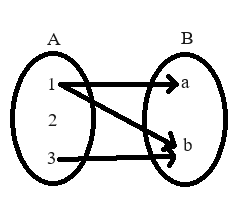
Cartesian Product

Cartesian Product or cross product of two non-empty sets $A$ and $B$ expressed as $A\times B$ is a set of all ordered pairs $(a,b)$, where $a\in A$, $b\in B$.

Mathematically it can be written as:

$$A\times B=\{(a,b)|a\in A,b\in B\}$$

E.g.: Considering $A=\{1,2\}$, $B=\{a,b,c\}$. Then the Cartesian Product is, $A\times B=\{(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)\}$.

Figure 1: Relation map for $A\times B$:

Binary Relation

Let $A$ and $B$ be two non-empty sets. A binary relation $R$ is a subset of $A\times B$, i.e., $R\subseteq A\times B$. If $(a,b)\in R$, then it is written as $aRb$.

Considering $A=\{1,2,3\}$, $B=\{a,b\}$, then $R$ could be, $R=\{(1,a),(1,b),(3,b)\}$.

Figure 2: Relation map for $aRb$:

Example 1: Let $A=\{2,3,4,5,6\}$. Define a relation $aRb$ such that $a$ divides $b$.

Given, $A=\{2,3,4,5,6\}$. The relation $aRb$, such that $a$ divides $b$ is:

$$aRb=\{(2,2),(2,4),(2,6),(3,3),(3,6),(4,4),(5,5),(6,6)\}$$

Example 2: Let $A=\{0,1,2,3,4\}$. Define a relation $aRb$ such that $a+b=4$.

Given, $A=\{0,1,2,3,4\}$. The relation $aRb$ such that, $a+b=4$, is:

$$aRb=\{(0,4),(1,3),(2,2),(3,1),(4,0)\}$$

Matrix of a relation

The matrix of a relation $A\times B$, where $A$ has $n$ elements, and $B$ has $m$ elements, is an $n\times m$ matrix, $M_R$ defined as follows:

$$M_R=[m_{ij}]$$

It can be perceived that:

$m_{ij}=1$, if $(a_i,b_j)\in R$, and

$m_{ij}=0$, if $(a_i,b_j)\notin R$.

E.g.: Considering $A=\{1,2,3\}$, $B=\{a,b,c,d\}$, and $aRb=\{(1,a),(2,a),(3,b),(3,d)\}$. Then their matrix, $M_R$ is:

$$M_R={\begin{bmatrix} 1&0&0&0\\ 1&0&0&0\\ 0&1&0&1\\ \end{bmatrix}}$$

While drawing matrix, the first element in the relation is taken as the row, and the second element is taken as the column.

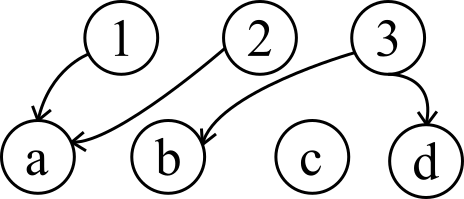
Di-graph

Di-graph stands for directed graph. It is used to map out the relation between elements of sets. Considering a relation $aRb=\{(1,a),(2,a),(3,b),(3,d)\}$, we have the following di-graph, for it:

Example 3: Let $A=\{0,1,2,3,4\}$. Define a relation $aRb$, such that $a+b=4$. Define its relation matrix and draw its di-graph.

For the set $A=\{0,1,2,3,4\}$, we have a relation such that $a+b=4$. Therefore we have, $aRb=\{(0,4),(1,3),(2,2),(3,1),(4,0)\}$. It's relation matrix $M_R$ is:

$$M_R= \begin{bmatrix} 0&0&0&0&1\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&1&0&0&0\\ 1&0&0&0&0 \end{bmatrix}$$

Di-graph for the above relation $aRb$ is:

Example 4: Let $A=\{0,1,2,3,4\}$. Define a relation $aRb$ such that HCF of $(a,b)$ is $1$.

Given, $A=\{0,1,2,3,4\}$. A relation, $aRb$, such that HCF of $(a,b)$ is $1$, is:

$$aRb=\{(1,1),(1,2),(1,3),(1,4),(2,1),(2,3),(3,1),(3,2),(3,4),(4,1),(4,3)\}$$ $$M_R= \begin{bmatrix} 0&0&0&0&0\\ 0&1&1&1&1\\ 0&1&0&1&0\\ 0&1&1&0&1\\ 0&1&0&1&0 \end{bmatrix}$$

flowchart LR
    A((0))
    B((1))-->B
    B-->C
    B-->D
    B-->E
    C((2))-->B
    C-->D
    D((3))-->B
    D-->C
    D-->E
    E((4))-->B
    E-->D

Properties of Relations

1. Reflexive: There should be $aRa$ for all $a\in A$.

2. Symmetric: If $aRb$ exists then $bRa$ should also exist for all $(a,b)\in A$.

3. Antisymmetric: If $aRb$ exists, then $bRa$ must not exist, but $bRa$ can exist if $a=b$ and $(a,b)\in A$.

4. Asymmetric: If $aRb$ exist, then $bRa$ must not exist for all $(a,b)\in A$,

5. Transitive: If $aRb$ and $bRc$ exists, then $aRc$ must exist where, $(a,b,c)\in A$.

Equivalence Relation

A binary relation $R$ on set $A$ is called an equivalence relation if $R$ is reflexive, symmetric and transitive.

E.g. Let $A=\{1,2,3\}$ and $R=\{(1,1),(1,2),(2,1),(2,2),(3,2)\}$. To check whether $R$ is reflexive or not, the following conditions must hold true:

$$M_R= \begin{bmatrix} 1&1&0\\ 1&1&0\\ 0&0&1 \end{bmatrix}$$

Test for reflexive:

Since, all elements in the right bearing diagonal are $1$, therefore, the relation is reflexive.

Test for symmetric:

$$M_R^{-1}= \begin{bmatrix} 1&1&0\\ 1&1&0\\ 0&0&1 \end{bmatrix}$$

Since, $M_R^{-1}=M_R$, therefore, the relation is symmetric.

Test for transitive:

$$(M_R)^2_\odot= \begin{bmatrix} 1&1&0\\ 1&1&0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} 1&1&0\\ 1&1&0\\ 0&0&1 \end{bmatrix} =\begin{bmatrix} 1&1&0\\ 1&1&0\\ 0&0&1 \end{bmatrix}$$

Since, $(M_R)^2_\odot=M_R$, therefore, the relation is transitive.

Since the relation $R$, is reflexive, symmetric and transitive, therefore, it is an equivalence relation.

Example 5: Let, $A={1,2,3}$, and $R=\{(1,1),(2,2),(2,3),(3,2),(3,3)\}$. Find out if $R$ is an equivalence relation or not.

For $R$ to be an equivalence relation, it must be reflexive, symmetric and transitive.

The matrix for $R$, $M_R$ is:

$$M_R= \begin{bmatrix} 1&0&0\\ 0&1&1\\ 0&1&1 \end{bmatrix}$$

Test for reflexive:

Since all the right bearing diagonals are $1$, therefore, the relation is reflexive.

Test for symmetric:

$$M_R^{-1}= \begin{bmatrix} 1&0&0\\ 0&1&1\\ 0&1&1 \end{bmatrix}$$

Since, $M_R^{-1}=M_R$, therefore, the relation is symmetric.

Test for transitive:

$$(M_R)^2_\odot= M_R= \begin{bmatrix} 1&0&0\\ 0&1&1\\ 0&1&1 \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&1&1\\ 0&1&1 \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 0&1&1\\ 0&1&1 \end{bmatrix}$$

Since, $(M_R)^2_\odot=M_R$, therefore, the relation is transitive.

Since the relation R, is reflexive, symmetric and transitive, therefore, it is an equivalence relation.

Closure

Certain elements added to the relation set to make it obey properties like reflexive, symmetry etc., is known as a relation closure.

E.g.: $A=\{0,1,2,3\}$, and $R=\{(0,1),(1,1),(1,2),(2,0),(2,2),(3,0)\}$.

Matrix of the relation, $M_R$ is:

$$M_R= \begin{bmatrix} 0&1&0&0\\ 0&1&1&0\\ 1&0&1&0\\ 1&0&0&0 \end{bmatrix}$$

Reflexive closure:

In order for $R$ to be reflexive, all right-bearing diagonal elements should be $1$. If $(0,0)$ and $(3,3)$ is added, the relation will be reflexive. Therefore reflexive closure $R'$, is:

$$R'=\{(0,1),(1,1),(1,2),(2,0),(2,2),(3,0),(0,0),(3,3)\}$$

Symmetric closure:

To find the symmetric closure, we derive $R^{-1}$, and perform $R\cup R^{-1}$.

$$R^{-1}=\{(1,0),(1,1),(2,1),(0,2),(2,2),(0,3)\}$$

Therefore, symmetric closure, $R'$, is:

$$R'=R\cup R^{-1}=\{(0,1),(1,1),(1,2),(2,0),(2,2),(3,0),(1,0),(2,1),(0,2),(0,3)\}$$

Transitive closure:

Transitive closure is performed using Warshall's Algorithm.

Considerin a set $A=\{1,2,3,4\}$, and $R=\{(2,1),(2,3),(3,1),(3,4),(4,1),(4,3)\}$. Then, its matrix is:

$$M_R= \begin{bmatrix} 0&0&0&0\\ 1&0&1&0\\ 1&0&0&1\\ 1&0&1&0 \end{bmatrix}$$

C	R	C.P.
$\{2,3,4\}$	$\{\phi\}$	-
$\{\phi\}$	$\{1,3\}$	-
$\{2,4\}$	$\{1,4\}$	$\{(2,1),(2,4),(4,1),(4,4)\}$
$\{3\}$	$\{1,3\}$	$\{(3,1),(3,3)\}$

$$M_R'= \begin{bmatrix} 0&0&0&0\\ 1&0&1&1\\ 1&0&1&1\\ 1&0&1&1 \end{bmatrix}$$

C	R	C.P.
$\{2,3,4\}$	$\{\phi\}$	-
$\{\phi\}$	$\{1,3,4\}$	-
$\{2,3,4\}$	$\{1,3,4\}$	$\{(2,1),(2,3),(2,4),(3,1),(3,3),(3,4),(4,1),(4,3),(4,4)\}$
$\{2,3,4\}$	$\{1,3,4\}$	$\{(2,1),(2,3),(2,4),(3,1),(3,3),(3,4),(4,1),(4,3),(4,4)\}$

$$M_R''= \begin{bmatrix} 0&0&0&0\\ 1&0&1&1\\ 1&0&1&1\\ 1&0&1&1 \end{bmatrix}$$

Since, $M_R'=M_R''$, therefore, transitive closure, $R'$ is:

$$R'=\{(2,1),(2,3),(2,4),(3,1),(3,3),(3,4),(4,1),(4,3),(4,4)\}$$

Example 6: Given the set $A=\{a,b,c,d\}$, and $R=\{(a,d),(b,a),(b,c),(c,a),(c,d),(d,c)\}$.

It's matrix is:

$$M_R= \begin{bmatrix} 0&0&0&1\\ 1&0&1&0\\ 1&0&0&1\\ 0&0&1&0 \end{bmatrix}$$

C	R	C.P.
$\{b,c\}$	$\{d\}$	$\{(b,d),(c,d)\}$
$\{\phi\}$	$\{a,c\}$	-
$\{b,d\}$	$\{a,d\}$	$\{(b,a),(b,d),(d,a),(d,d)\}$
$\{a,c\}$	$\{c\}$	$\{(a,c),(c,c)\}$

$$M_R'= \begin{bmatrix} 0&0&1&1\\ 1&0&1&1\\ 1&0&1&1\\ 1&0&1&1 \end{bmatrix}$$

C	R	C.P.
$\{b,c,d\}$	$\{c,d\}$	$\{(b,c),(b,d),(c,c),(c,d),(d,c),(d,d)\}$
$\{\phi\}$	$\{a,c,d\}$	-
$\{a,b,c,d\}$	$\{a,c,d\}$	$\{(a,a),(a,c),(a,d),(b,a),(b,c),(b,d),(c,a),(c,c),(c,d),(d,a),(d,c),(d,d)\}$
$\{a,b,c,d\}$	$\{a,c,d\}$	$\{(a,a),(a,c),(a,d),(b,a),(b,c),(b,d),(c,a),(c,c),(c,d),(d,a),(d,c),(d,d)\}$

$$M_R''= \begin{bmatrix} 1&0&1&1\\ 1&0&1&1\\ 1&0&1&1\\ 1&0&1&1 \end{bmatrix}$$

C	R	C.P.
$\{a,b,c,d\}$	$\{a,c,d\}$	$\{(a,a),(a,c),(a,d),(b,a),(b,c),(b,d),(c,a),(c,c),(c,d),(d,a),(d,c),(d,d)\}$
$\{\phi\}$	$\{a,c,d\}$	-
$\{a,b,c,d\}$	$\{a,c,d\}$	$\{(a,a),(a,c),(a,d),(b,a),(b,c),(b,d),(c,a),(c,c),(c,d),(d,a),(d,c),(d,d)\}$
$\{a,b,c,d\}$	$\{a,c,d\}$	$\{(a,a),(a,c),(a,d),(b,a),(b,c),(b,d),(c,a),(c,c),(c,d),(d,a),(d,c),(d,d)\}$

$$M_R'''= \begin{bmatrix} 1&0&1&1\\ 1&0&1&1\\ 1&0&1&1\\ 1&0&1&1 \end{bmatrix}$$

Since, $M_R''=M_R'''$, therefore, transitive closure, $R'$ is achieved.

$$R'=\{(a,a),(a,c),(a,d),(b,a),(b,c),(b,d),(c,a),(c,c),(c,d),(d,a),(d,c),(d,d)\}$$

Equivalence of class and partition

The general equation for equivalent classes:

$$[x]=\{y|y\in A,(x,y)\in R\}$$

E.g.: $A=\{1,2,3,4,5\}$, and $R=\{(1,1),(2,2),(3,3),(4,4),(5,5),(1,2),(2,1),(4,5),(5,4)\}$

$$[1]=\{1,2\}, [2]=\{2,1\}, [3]=\{3\}, [4]=\{4,5\}, [5]=\{5,4\}$$

Therefore, the partitions are:

$P_1=\{1,2\}$, $P_2=\{3\}$, $P_3=\{4,5\}$

From the above, it can be drawn out that:

$$P_1\cup P_2\cup P_3=A$$ $$P_1\cap P_2\cap P_3 = \{\phi\}$$

Example 7: $A=\{1,2,3\}$, and $R=\{(1,1),(1,2),(2,1),(2,2),(3,3)\}$.

Equivalence classes:

$$[1]=\{1.2\}, [2]=\{2,1\}, [3]=\{3\}$$

Partitions are:

$P_1=\{1,2\}$, $P_2=\{3\}$

Example 8: Let set $A=\{1,2,3,4,5,6\}$, $P_1=\{1,3,5\}$, $P_2=\{2,4,6\}$, where $P_1$, and $P_2$ are partitions. Find the relation set of the set $A$.

$R$ could be found by the union of the Cartesian products of the two partitions.

$$R=\{(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),\\(2,2),(2,4),(2,6),(4,2),(4,4),(4,6),(6,2),(6,4),(6,6)\}$$

POSET

POSET stands for partial-order set. Let $R$ be a relation on set $A$. The relation $R$ is called partial order set (POSET), if $R$ is reflexive, antisymmetric, and transitive. A POSET is symbolically represented as $(A,\le)$.

E.g.: Let a set be $A=\{1,2,3,4\}$, and its relation set be defined by $R=\{(a,b)|(a,b)\in A, a\ge b\}$.

$$R=\{(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4)\}$$

It's relation matrix is:

$$M_R= \begin{bmatrix} 1&0&0&0\\ 1&1&0&0\\ 1&1&1&0\\ 1&1&1&1 \end{bmatrix}$$

Check for reflexive:

Since all diagonal elements are $1$, therefore the relation is reflexive.

Check for antisymmetric:

For all non-diagonal elements, $[m_{ij}]=1$, $[m_{j,i}=0]$, hence it is antisymmetric.

Check for transitive:

$$(M_R)^2_\odot= \begin{bmatrix} 1&0&0&0\\ 1&1&0&0\\ 1&1&1&0\\ 1&1&1&1 \end{bmatrix} \begin{bmatrix} 1&0&0&0\\ 1&1&0&0\\ 1&1&1&0\\ 1&1&1&1 \end{bmatrix} = \begin{bmatrix} 1&0&0&0\\ 1&1&0&0\\ 1&1&1&0\\ 1&1&1&1 \end{bmatrix}$$

Since, $(M_R)^2_\odot=M_R$, therefore the relation is transitive.

Since the relation is reflexive, antisymmetric, and transitive, therefore the relation is a POSET.