Binary logic deals with vairables that take two discrete values — 1 for TRUE and 0 for FALSE. A simple switching circuit containing active elements such as diode and the transistor can demonstrate the binary logic, which can either be ON (switch closed) or OFF (switch open). Electrical signals such as voltage or current exist throughout the digital system in either one of the two recognizable voltages, except during the transition.

Representations

• $\bar{A}=\textnormal{NOT}$
• $A+B=\textnormal{OR}$
• $A.B=\textnormal{AND}$

Formulae

1. $A+A=A$
   $A.A=A$
2. $A+\bar{A}=1$
   $A.\bar{A}=0$
3. $A+0=A$
   $A.0=0$
4. $A+1=1$
   $A.1=A$
5. $\bar{\bar{A}}=A$
6. $A+AB=A$
7. $(A+B)(A+C)=A+BC$
8. $A+\bar{A}B=A+B$

Example 1: Prove $AB+\bar{A}C+BC=AB+\bar{A}C$

Solution:

$$\begin{align*} \textnormal{LHS}&=AB+\bar{A}C+BC\\ &=AB+\bar{A}C+BC(A+\bar{A}) && [\because X+\bar{X}=1]\\ &=AB+\bar{A}C+ABC+\bar{A}BC\\ &=AB(1+C)+\bar{A}C(1+B)\\ &=AB+\bar{A}C && [\because 1+X=1]\\ &=\textnormal{RHS} \end{align*}$$

Therefore, proved.

Example 2: Prove $A+\bar{A}B=A+B$ using truth table.

Solution:

$A$	$B$	$\bar{A}B$	$A+\bar{A}B$	$A+B$
0	0	0	0	0
0	1	1	1	1
1	0	0	1	1
1	1	0	1	1

Since the columns $A+\bar AB$ is equal to $A+B$, therefore, the truth table holds.

Example 3: Prove $\bar{A}\bar{B}\bar{C}+\bar{A}B\bar{C}+A\bar{B}\bar{C}+AB\bar{C}=\bar{C}$

Solution:

$$\begin{align*} \text{LHS}&=\bar{A}\bar{B}\bar{C}+\bar{A}B\bar{C}+A\bar{B}\bar{C}+AB\bar{C}\\ &=\bar{A}\bar{C}(\bar{B}+B)+A\bar{C}(\bar{B}+B)\\ &=\bar{A}\bar{C}+A\bar{C} && [\because \bar{X}+X=1]\\ &=\bar{C}(\bar{A}+A)\\ &=\bar{C} && [\because \bar{X} + X=1]\\ &=\text{RHS} \end{align*}$$

Example 4: Prove $AB+\bar{A}+\bar{C}+A\bar{B}C(AB+C)=1$

Solution:

$$\begin{align*} \text{LHS}&=AB+\bar{A}+\bar{C}+A\bar{B}C(AB+C)\\ &=B+\bar{A}+\bar{C}+A\bar{B}(AB+C)&&[\because X+\bar{X}Y=X+Y]\\ &=B+A(AB+C)+\bar{A}+\bar{C}&&[\because X+\bar{X}Y=X+Y]\\ &=B+AB+C+\bar{A}+\bar{C}&&[\because X+\bar{X}Y=X+Y]\\ &=B+AB+\bar{A}+1&&[\because X+\bar{X}=1]\\ &=1&&[\because X+1=1]\\ &=\text{RHS} \end{align*}$$

Example 5: Prove $\bar{A}B(\bar{D}+\bar{C}D)+B(A+\bar{A}CD)=B$

Solution:

$$\begin{align*} \text{LHS}&=\bar{A}B(\bar{D}+\bar{C}D)+B(A+\bar{A}CD)\\ &=\bar{A}B\bar{D}+\bar{A}B\bar{C}D+AB+\bar{A}BCD\\ &=\bar{A}B\bar{D}+AB+\bar{A}BD(\bar{C}+C)\\ &=\bar{A}B\bar{D}+AB+\bar{A}BD && [\because X+\bar{X}=1]\\ &=\bar{A}B(\bar{D}+D)+AB\\ &=\bar{A}B+AB && [\because X+\bar{X}=1]\\ &=B(\bar{A}+A)\\ &=B&&[\because \bar{X}+X=1]\\ &=\text{RHS} \end{align*}$$

Karnaugh Map

Karnaugh Map, in short K-map is used to minify boolean expressions. K-maps are made using $2^n$ square patterns. It can be used in two formats:

• SOP: Sum of products ($\bar{A}\bar{B}, \bar{A}B, AB, A\bar{B}$)
• POS: Product of sums ($A+B, A+\bar{B}, \bar{A}+\bar{B}, \bar{A}+B$)

Sum of products

For example, K-map for two entries is, $(A,B)=2^2=4$:

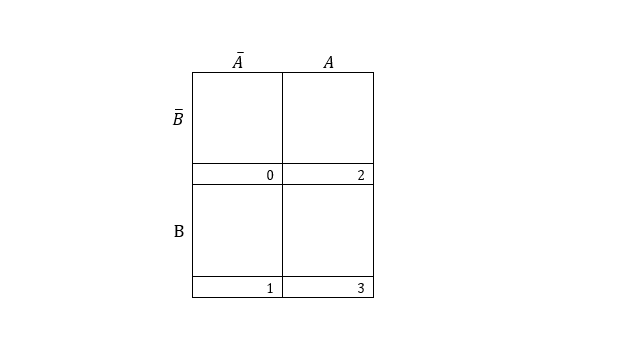
K-map for three entries is, $(A,B,C)=2^3=8$:

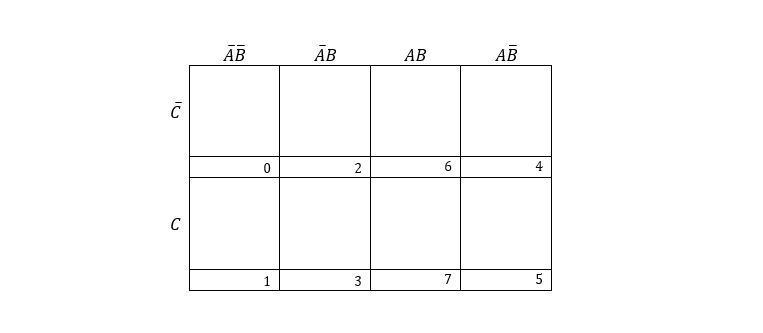
K-map for four entries is, $(A,B,C,D)=2^4=16$:

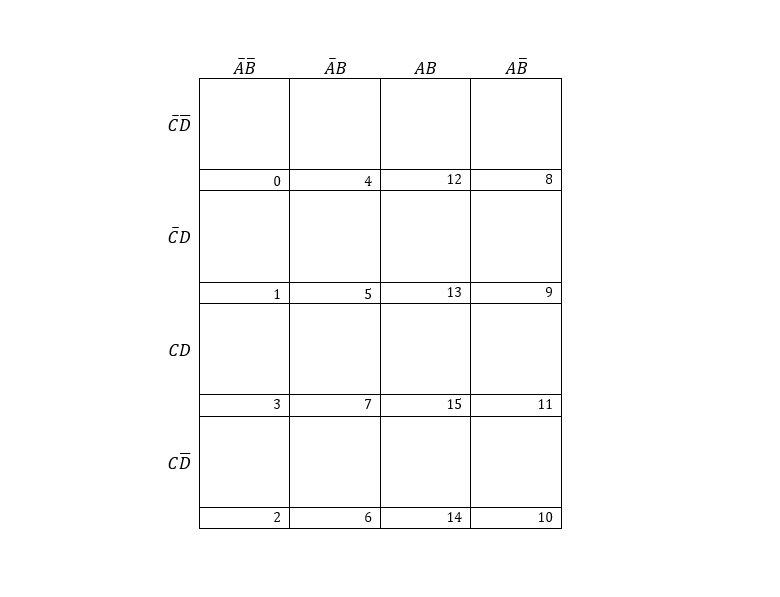
For each entry data is mapped, in the power of $2$ itself. Maximum number of entries are grouped, in the powers of base 2 in decending order, i.e., $\ldots 16,8,4,2$. A single entry can never be considered.

Example 6: Considering entries, $f=\sum{8,10,11,12,13,14,15}$, find the minimized expression using K-map.

K-map for the above entries is:

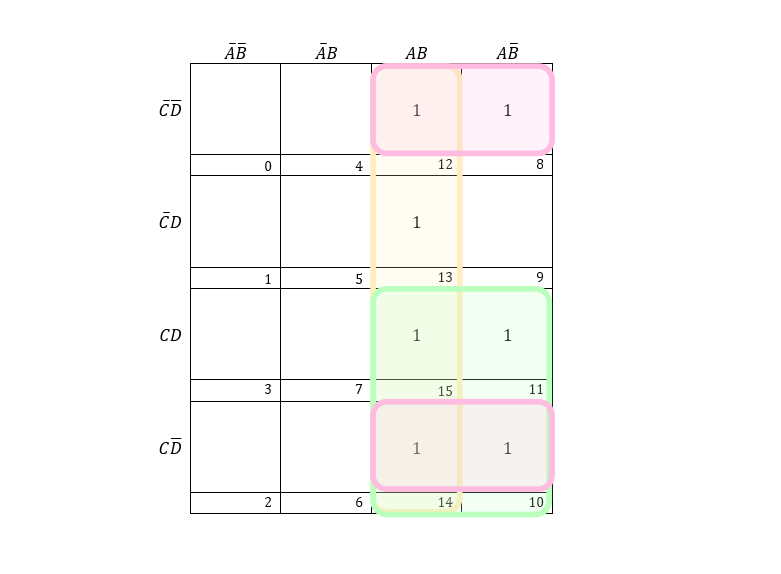
From the yellow region, the common variables are $AB$, the pink region has $A\bar{D}$ in common, and the green region has $AC$ in common. Therefore, the minimized result for the K-map is:

$$\text{Result}=AB+AC+A\bar{D}$$

Example 7: Considering entries, $f=\sum{7,9,10,11,12,13,14,15}$, find the minimized expression using K-map.

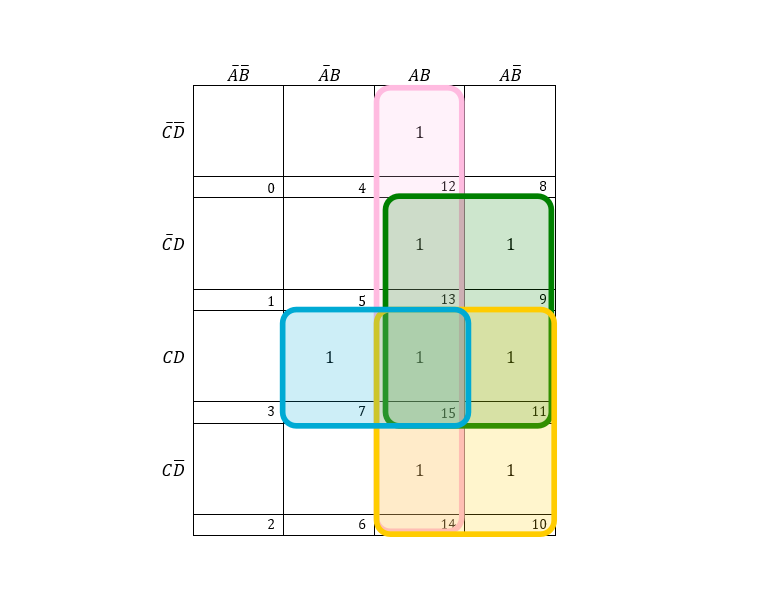
From, the pink region, we have $AB$, the green region has $AD$ in common, the blue region has $BCD$ in common, and the wellow region has $AC$ in common.

$$\therefore \text{Result}=AB+AD+AC+BCD$$

Don't care condition, is when entries have no effect on the minimization but can be used to help pair other entries are called don't care entries.

Example 8: Considering entries, $f(A,B,C,D)=\displaystyle\sum_m{(1,3,7,11,15)}+\displaystyle\sum_d{(0,2,5)}$, find the minimized expression using K-map.

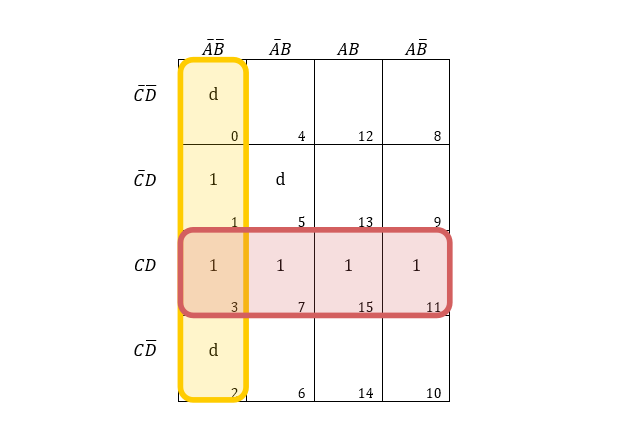
From the red region, we have $CD$ as common, and from the yellow region, we have $\bar{A}\bar{B}$ as common.

$$\therefore \text{Result}=\bar{A}\bar{B}+CD$$

Example 9: Considering entries, $f(A,B,C,D)=\displaystyle\sum_m{(0,2,3,6,7)}+\displaystyle\sum_d{(8,10,11,15)}$, find the minimized expression using K-map.

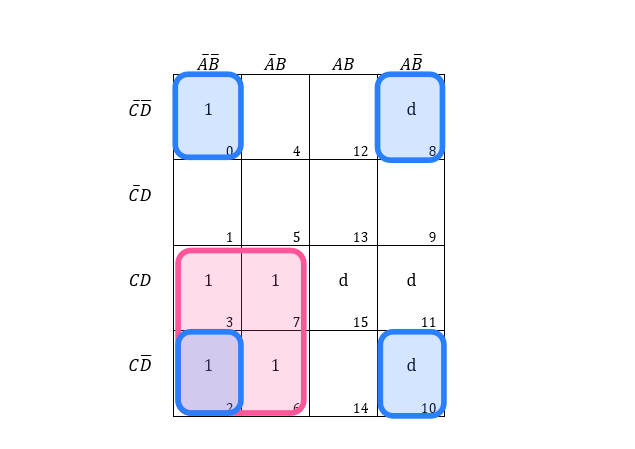
From the pink region, we have $\bar{A}C$ common, and from blue regions in the corners, we have $\bar{B}\bar{D}$ as common.

$$\therefore\text{Result}=\bar{A}C+\bar{B}\bar{D}$$

Product of sums

In sum of products, we consider the entries as 1 to perform operations, but in case of product of sums, we consider the entries as 0 to perform operations.

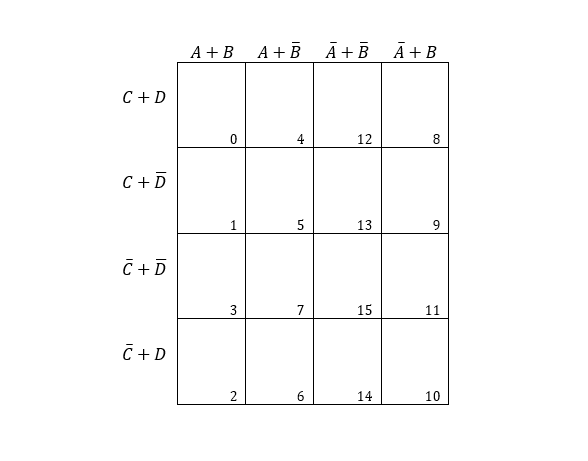
K-map for four entries in products of sum i.e, $f(A,B,C,D)$ is:

Example 10: Considering entries, $f(A,B,C,D)=\pi(1,3,5,7,9,10,12,13)$, find the minimized expression using K-map.

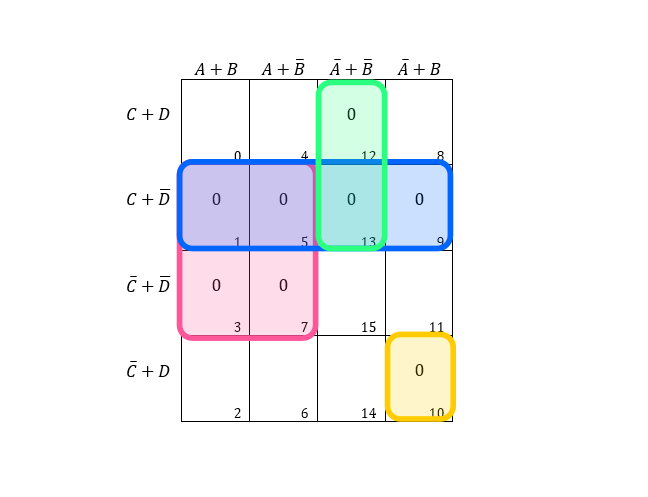
From the blue region, we can get the sum as $C+\bar{D}$. From the red region we get the sum as, $A+\bar{D}$, from the green region, we get, $\bar{A}+\bar{B}+C$, and from the yellow region, we have $\bar{A}+B+\bar{C}+D$.

$$\therefore\text{Result}=(\bar{A}+\bar{B}+C).(C+\bar{D}).(A+\bar{D}).(\bar{A}+B+\bar{C}+D)$$

Example 11: Considering entries, $f(A,B,C,D)=\pi_m(0,2,3,5,7,8,13)+\pi_d(1,6,12)$, find the minimized expression using K-map.

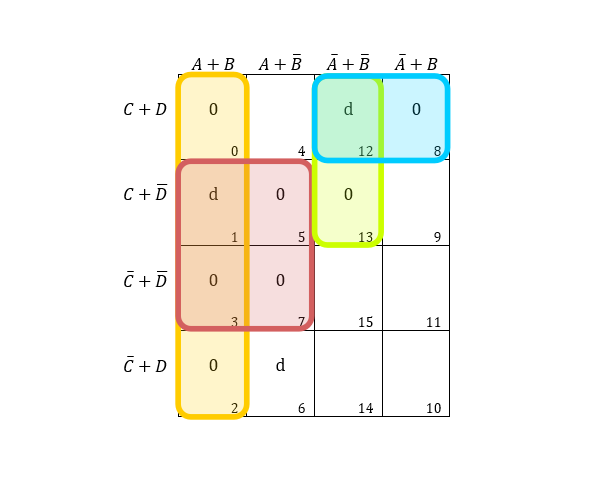
From the yellow region, we have $A+B$, the red region gives, $A+\bar{D}$, the blue region gives, $\bar{A}+C+D$, and the green region gives, $\bar{A}+\bar{B}+C$.

$$\therefore\text{Result}=(A+B)(A+\bar{D})(\bar{A}+C+D)(\bar{A}+\bar{B}+C)$$

Example 12: A company has $100$ shares. There are four shareholders written as $f(x)=S$, where $x$ is the shareholder and $S$ is the number of shares. The four shareholders and their shares are: $f(A)=40$, $f(B)=30$, $f(C)=20$, $f(D)=10$. Make a digital circuit such that the resolution will be passed if $2/3$-rd of the vote is for it.

Solution:

Equivalent votes required to pass a resolution:

$$v_e=\frac{2}{3}\times100=66.67\approx67$$

Truth table for votes and resolution passing:

A	B	C	D	P	E
0	0	0	0	0	0
0	0	0	1	0	1
0	0	1	0	0	2
0	0	1	1	0	3
0	1	0	0	0	4
0	1	0	1	0	5
0	1	1	0	0	6
0	1	1	1	0	7
1	0	0	0	0	8
1	0	0	1	0	9
1	0	1	0	0	10
1	0	1	1	1	11
1	1	0	0	1	12
1	1	0	1	1	13
1	1	1	0	1	14
1	1	1	1	1	15

where, P is the passing of resolution, and E is the equivalent digit

K-map for the circuit:

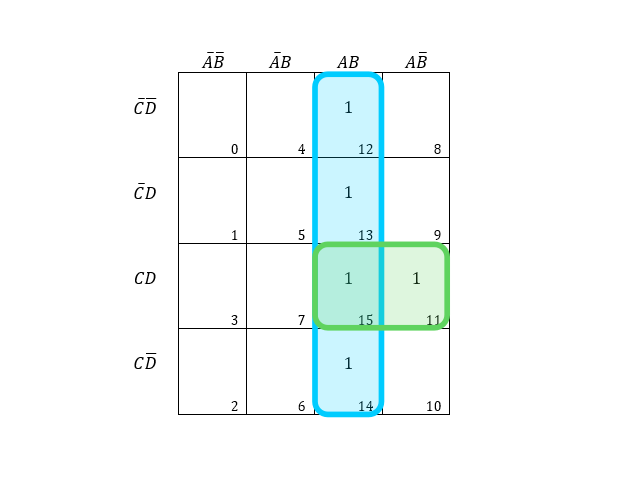
From the blue region, we have $AB$ has common, and in the green region, we have $ACD$ as common.

Therefore, the circuit result is:

$$\text{Result}=AB+ACD$$

De-Morgan's theorem

De-Morgan's theorem, has the following operations:

• $\overline{A+B}=\bar{A}.\bar{B}$

• $\overline{A.B}=\bar{A}+\bar{B}$

Example 13: Evaluate $\overline{(\bar{A}+\bar{B}C).(\overline{AB}+C)}$

$$\begin{align*} \text{Expression}&=\overline{(\bar{A}+\bar{B}C).(\overline{AB}+C)}\\ &=\overline{(\bar{A}+\bar{B}C)}+\overline{(\overline{AB}+C)}\\ &=\overline{\bar{A}}.\overline{\bar{B}C}+\overline{\overline{AB}}.\bar{C}\\ &=A.(B+\bar{C})+AB\bar{C} \end{align*}$$

Example 14: Evaluate $\overline{(AB+\bar{C}).(\overline{A+B}+C)+\bar{A}B}$

$$\begin{align*} \text{Expression}&=\overline{(AB+\bar{C}).(\overline{A+B}+C)+\bar{A}B}\\ &=\{\overline{(AB+\bar{C}).(\overline{A+B}+C)}\}.(\overline{\bar{A}B})\\ &=\{\overline{(AB+\bar{C})}+\overline{(\overline{A+B}+C)}\}.(\bar{\bar{A}}+\bar{B})\\ &=\{(\overline{AB}.\bar{\bar{C}})+(\overline{\overline{A+B}}).\bar{C}\}.(A+\bar{B})\\ &=\{(\bar{A}+\bar{B}).C+(A+B).\bar{C}\}.(A+\bar{B}) \end{align*}$$

Prove that: $(A+B)(\bar{A}\bar{C}+C)(\overline{\bar{B}+AC})=\bar{A}B$

$$\begin{align*} \text{LHS}&=(A+B)(\bar{A}\bar{C}+C)(\overline{\bar{B}+AC})\\ &=(A+B)(\bar{A}+C)(\bar{\bar{B}}.\overline{AC})&[\because \bar{X}Y+X=Y+X]\\ &=(A+B)(\bar{A}+C)\{B(\bar{A}+\bar{C})\}\\ &=(A\bar{A}+AC+\bar{A}B+BC)(\bar{A}+\bar{C})B\\ &=(AC+\bar{A}B+BC)(\bar{A}B+B\bar{C})&[\because \bar{X}.X=0]\\ &=\bar{A}ABC+\bar{A}B+\bar{A}BC+ABC\bar{C}+\bar{A}B\bar{C}+BC\bar{C}\\ &=\bar{A}B+\bar{A}B(C+\bar{C})\\ &=\bar{A}B+\bar{A}B&[\because X+\bar{X}=1]\\ &=\bar{A}B\\ &=\text{RHS} \end{align*}$$