Following are the interactive versions of the circuits used in the document:

Arithmetic circuits are used to perform several different arithmetic operations using a single composite circuit. Half adder, subtractors etc., are examples of arithmetic circuits.

Half Adder

Half adder is an arithmetic circuit that performs arithmetic addition of two binary digits. Following is the details of a half adder.

Block diagram

Truth table

A	B	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Circuit diagram

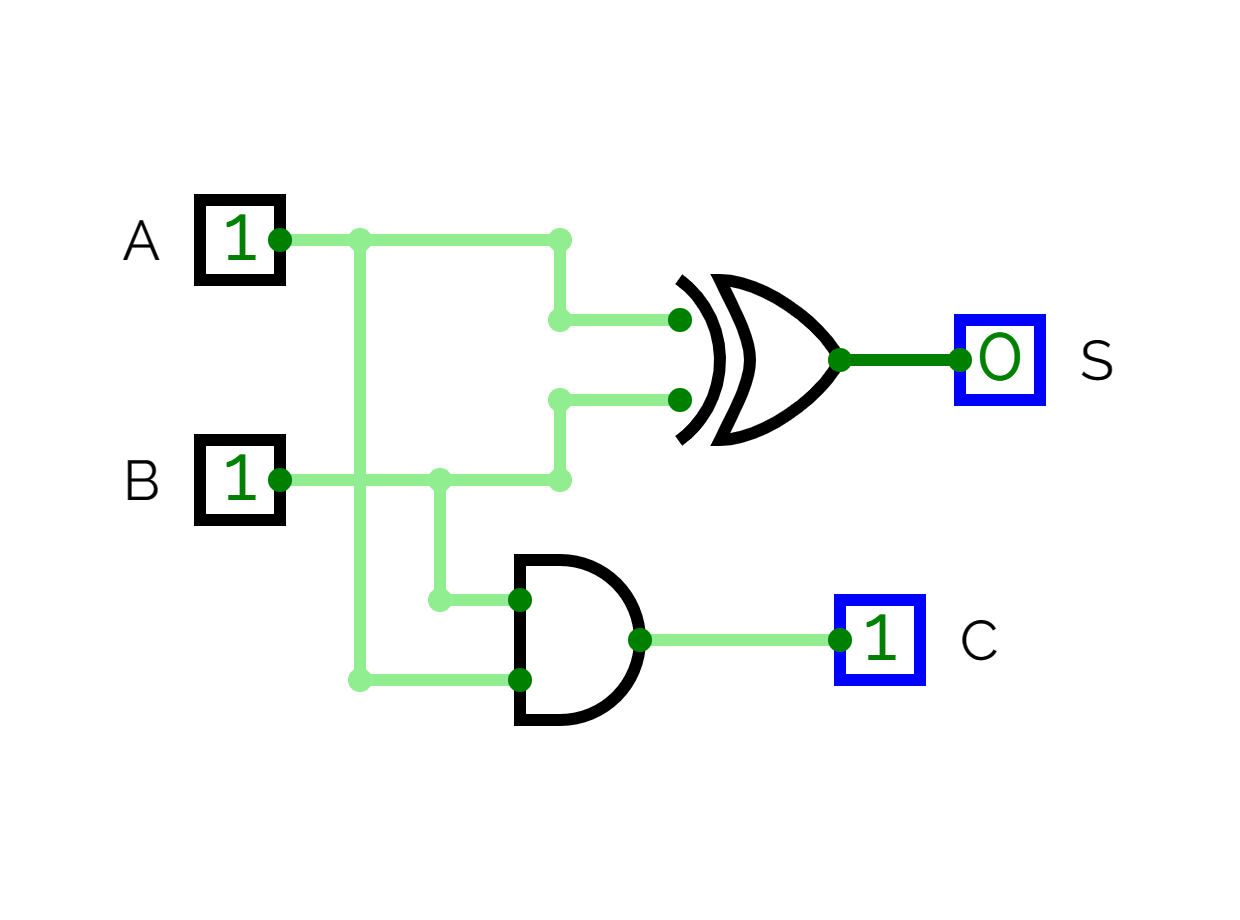
Working

• It has two inputs $A$ and $B$, and two outputs sum $S$, and carry $C$.

• The sum is derived with XOR operation on the inputs:

  $$\begin{align*} S&=A\oplus B\\ &=\bar{A}B+A\bar{B} \end{align*}$$

• The carry is generated by AND operation on the inputs:

  $$C=A.B$$

Full Adder

A full adder is a combinational circuit that performs arithmetic sum of three input bits, $\{A,B,C\}$ and produces a sum $S$ and carry $C$.

Block diagram

Truth table

A	B	C	S	C
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Circuit diagram

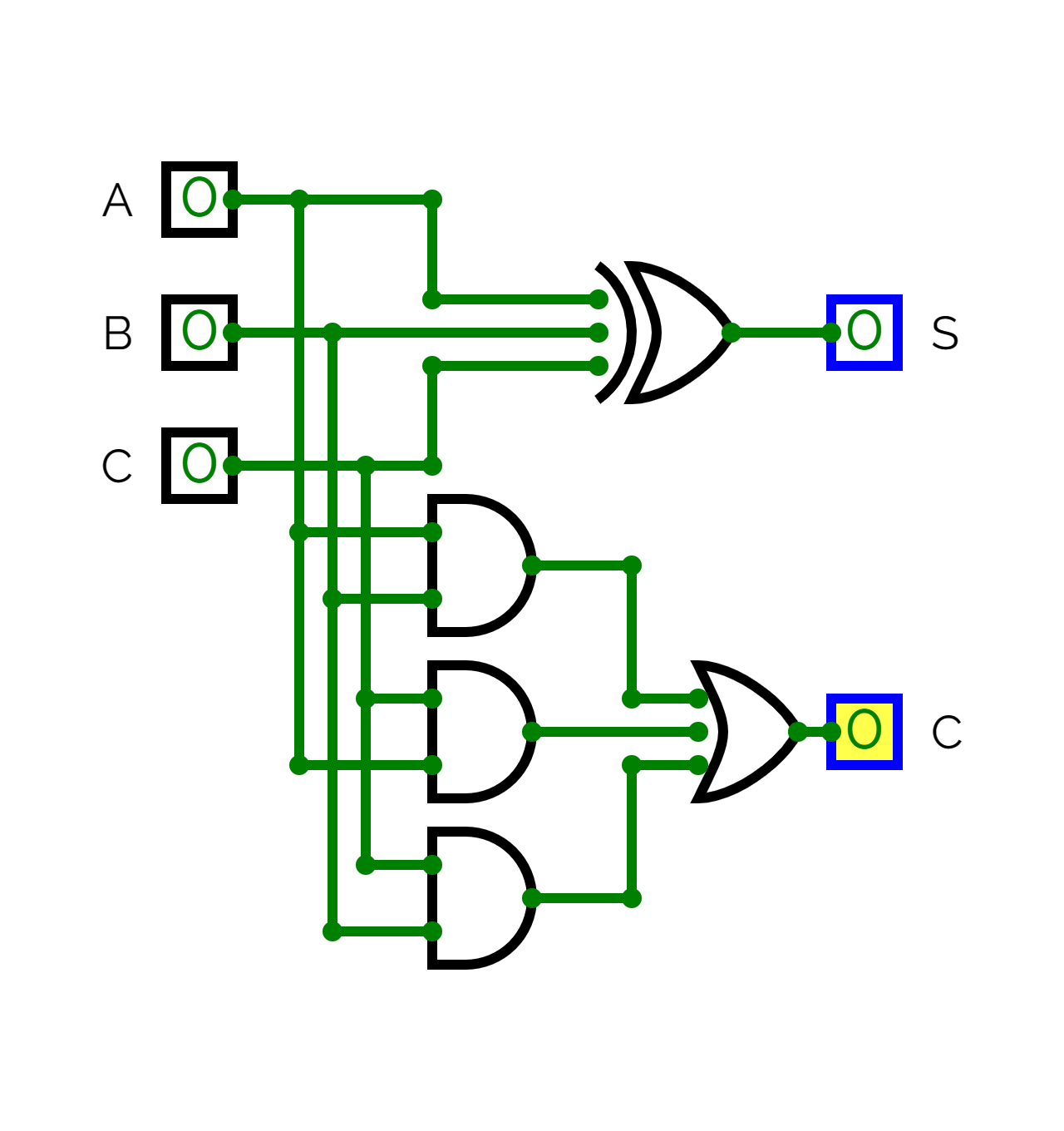
Working

• It consists of three inputs denoted by $A$ (augend bit), and $B$ (addend bit), and third input $C$, which represents the carry from the previous lower significant bit.

• It produces two outputs sum $S$, and carry $C$.

• From the above truth table using S.O.P. (sum of products), the formula of sum is derived as follows:

$$\begin{align*} S&=\bar{A}\bar{B}C+\bar{A}B\bar{C}+A\bar{B}\bar{C}+ABC\\ &=\bar{A}(\bar{B}C+B\bar{C})+A(\bar{B}\bar{C}+BC)\\ &=\bar{A}(B\oplus C)+A(\overline{B\oplus C})\\ &=A\oplus B\oplus C \end{align*}$$

• From the above truth table using S.O.P. the formula of carry is:

$$\begin{align*} S&=\bar{A}BC+A\bar{B}C+AB\bar{C}+ABC\\ &=\bar{A}BC+A\bar{B}C+AB(\bar{C}+C)\\ &=\bar{A}BC+A\bar{B}C+AB&&[\because\bar{x}+x=1]\\ &=B(\bar{A}C+A)+A\bar{B}C\\ &=BC+A(B+\bar{B}C)&&[\because\bar{x}y+x=y+x]\\ &=AB+BC+AC \end{align*}$$

4-bit Parallel Adder

This circuit is capable of adding two 4-bit binary numbers resulting in four bit sum and a carry.

Construction

Binary bits:

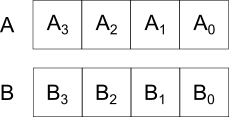
Design:

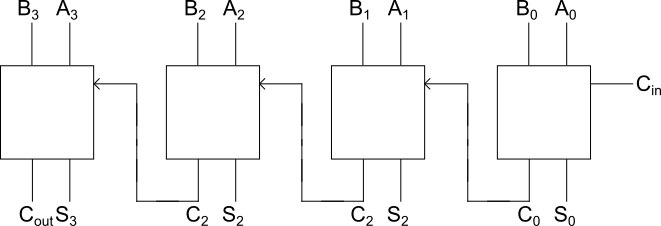
• Two 4-bit binary numbers are in storage $A$ and $B$.
• Four full adders are used.
• The $C_{in}$ input is always 0.
• $A_i$ and $B_i$ and carry from the significant bit is fed as input to produce sum $S_i$ and the carry generated is forwarded to the next full adder.
• $C_{\textnormal{out}}$ is the final carry

Working

• In least significant bit, $A_0$, $B_0$, and $C_{\textnormal{in}}$ (which is 0) are added to produce sum $S_0$ and carry $C_0$.
• Similarly all the other inputs are added in respective full adders.
• If no carry is generated 0 is forwarded.
• In case a fifth bit is generated in the final sum it is produced through $C_{\textnormal{out}}$.

4-bit Combined Paraller Adder/Subtractor

The 4-bit parallel adder/subtractor circuit is capable of performing both addition and subtraction on two binary numbers.

Construction

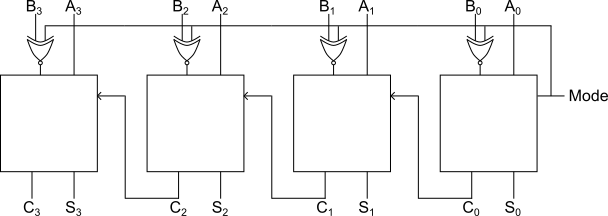
• Two 4-bit numbers are stored in storage $A$ and $B$.
• $A_i$ bits are fed into the full adders directly.
• The $B_i$ inputs are fed via XOR gates.
• The other input of XOR gate are kept common and connected to the input of first full adder known as mode.

Working

When mode is 0, we can understand the working if we concentrate on the first full adder, the inputs are:

$$\begin{align*} &A_0+(B_0\oplus0)+0\\ =\ &A_0+B_0&&[\because B_0 \oplus 0 =B_0] \end{align*}$$

Therefore, the circuit acts as an adder circuit.

But when mode is 1, the inputs are:

$$\begin{align*} &A_0+(\overline{B_0}\oplus1)\\ =\ &A_0+B_0&&[\because \overline{B_0}\oplus1=\overline{B_0}]\\ =\ &A_0+(\textnormal{2's compliment of }B_0)\\ =\ &A_0+(-B_0)\\ =\ &A_0-B_0 \end{align*}$$

Therefore, the circuit acts as a subtractor.

Half Subtractor

A half subtractor is an arithmatic circuit used to subtract two binary digits. It takes in two inputs $A$ and $B$, and returns two outputs: difference ($D$), and borrow ($B_0$).

Block diagram

Truth table

$A$	$B$	$C$	$B_0$
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

Circuit diagram

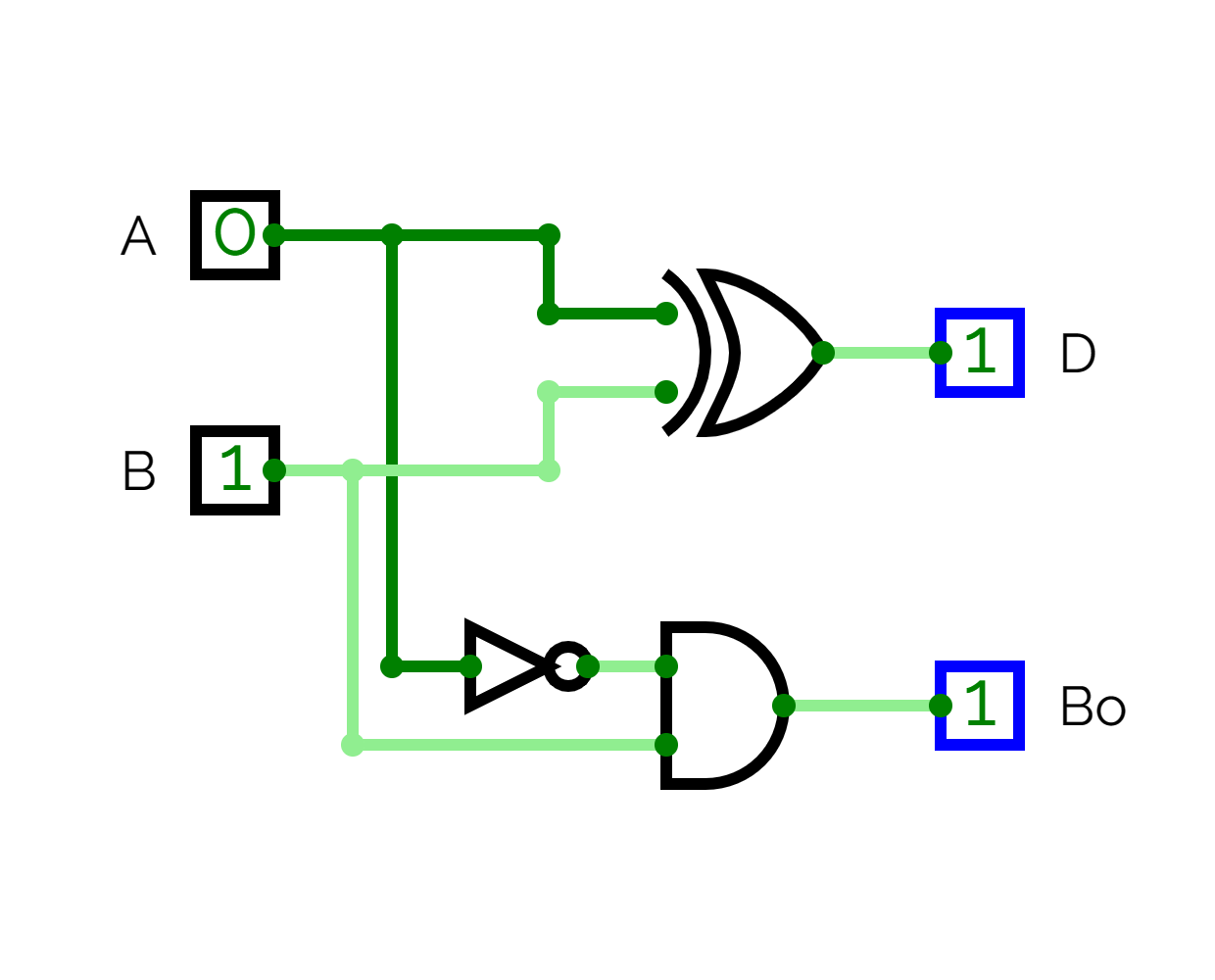
Construction

• Two inputs $A$ and $B$ are passed directly into the XOR gate which gives the difference $D$.
• The inputs from $A$ is first passed into the NOT gate then along with $B$ is passed into the AND gate giving the borrow $B_0$.

Working

• The formula for the difference can be brought out using the truth table:

  $$\begin{align*} D&=\bar{A}B+A\bar{B}\\ &=A\oplus B \end{align*}$$

  The above is a formula of a XOR gate.

• The formula for borrow can be brought out using truth table as:

  $$\begin{align*} B_0=\bar{A}B \end{align*}$$

Full Subtractor

A full subtractor accepts three input lines of binary digits and returns their difference and respective borrows.

Block diagram

Truth table

$A$	$B$	$C$	$D$	$B_0$
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

Circuit diagram

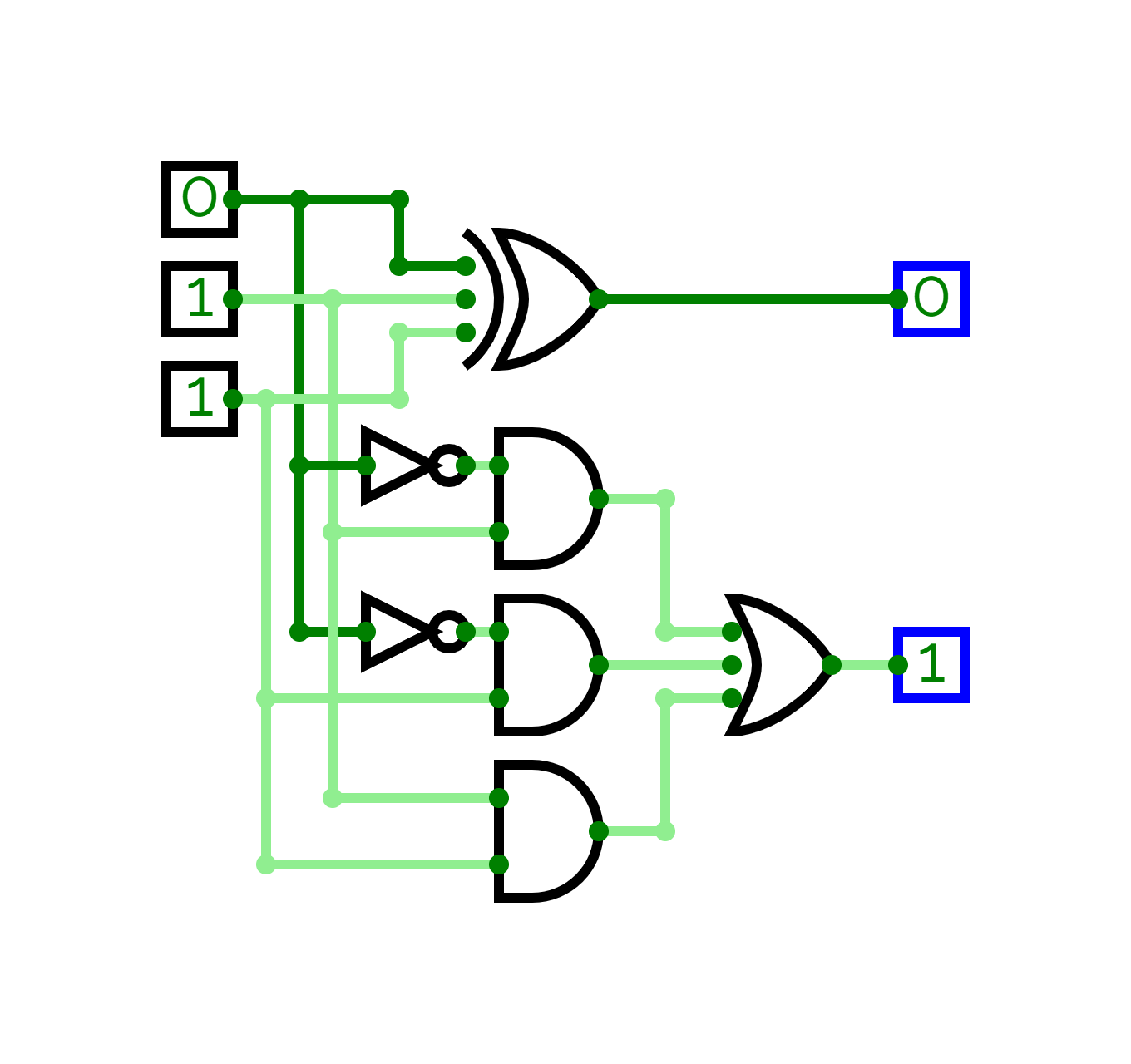
Construction

• There are three input lines, which are passed directly into the XOR gate, which gives us the difference $D$.
• And two consequetive lines from three input with each combination with a NOT gate through $A$, and noral lines through others are passed into respective AND gates to form, $\bar{A}B$, $\bar{A}C$, and $BC$ combinations.
• Finally the three combinations are passed into an OR gate to get the final borrow $B_0$

Working

• Using S.O.P., we can find the formula for difference from the truth table as:

  $$\begin{align*} D&=\bar{A}\bar{B}C+\bar{A}B\bar{C}+A\bar{B}\bar{C}+ABC\\ &=\bar{A}(\bar{B}C+B\bar{C})+A(\bar{B}\bar{C}+BC)\\ &=\bar{A}(B\oplus C)+A(\overline{B\oplus C})&&[\because \bar{x}y+x\bar{y}=x\oplus y\textnormal{ and, }\bar{x}\bar{y}+xy=\overline{x\oplus y}]\\ &=A\oplus B\oplus C&&[\because \bar{x}y+x\bar{y}=x\oplus y] \end{align*}$$

  Therefore, the result is that of a XOR gate

• Using K-map, the formula for borrow can be brought out as:

  

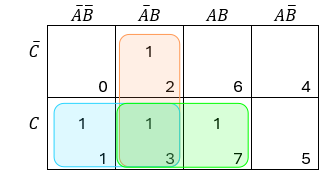
  From the blue region, we have $\bar{A}C$ as common, from yellow region, we have $\bar{A}B$ as common, and from the green region we have, $BC$ common.

  $$\begin{align*} B_0&=\bar{A}B+BC+\bar{A}C \end{align*}$$